Slope Of Best Fit Line

Line of Best Fit (Least Square Method)

A line of all-time fit is a straight line that is the best approximation of the given set of data.

It is used to study the nature of the relation between two variables. (We're just considering the 2-dimensional example, here.)

A line of best fit tin can be roughly adamant using an eyeball method by drawing a straight line on a besprinkle plot and so that the number of points above the line and below the line is about equal (and the line passes through every bit many points every bit possible).

A more authentic way of finding the line of all-time fit is the least square method .

Apply the following steps to find the equation of line of best fit for a set of ordered pairs $\left({\mathrm{ten}}_1,y_1\right),\left({\mathrm{10}}_2,y_2\right),\mathrm{...}\left(x_n,y_n\right)$ .

Step ane: Summate the hateful of the $x$ -values and the mean of the $y$ -values.

$\begin{array}{l}\overline{\mathrm{Ten}}=\frac{{\displaystyle \sum _{i=1}^{\mathrm{due\; north}}{\mathrm{ten}}_i}}{n}\\ \overline{Y}=\frac{{\displaystyle \sum _{i=\mathrm{ane}}^n{y}_i}}{n}\end{array}$

Footstep two: The following formula gives the slope of the line of best fit:

$m=\frac{{\displaystyle \sum _{i=\mathrm{ane}}^n\left({\mathrm{10}}_i-\overline{\mathrm{Ten}}\right)\left(y_i-\overline{Y}\right)}}{{\displaystyle \sum _{i=\mathrm{i}}^{\mathrm{north}}{\left(x_i-\overline{X}\right)}^2}}$

Pace 3: Compute the $y$ -intercept of the line by using the formula:

$b=\overline{Y}-m\overline{\mathrm{10}}$

Pace 4: Use the slope $m$ and the $y$ -intercept $b$ to grade the equation of the line.

Example:

Use the least square method to determine the equation of line of all-time fit for the data. And then plot the line.

$\mathrm{ten}$	$8$	$2$	$\mathrm{eleven}$	$\mathrm{six}$	$\mathrm{v}$	$4$	$12$	$9$	$6$	$\mathrm{one}$
$y$	$3$	$\mathrm{ten}$	$\mathrm{iii}$	$6$	$\mathrm{viii}$	$12$	$1$	$4$	$9$	$14$

Solution:

Plot the points on a coordinate plane .

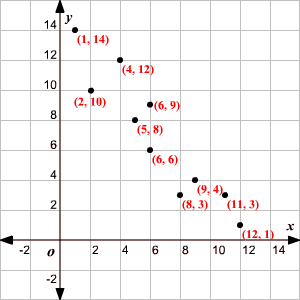
Calculate the means of the $\mathrm{ten}$ -values and the $y$ -values.

$\begin{array}{l}\overline{\mathrm{Ten}}=\frac{8+2+11+\mathrm{half\; dozen}+5+\mathrm{four}+12+9+6+1}{\mathrm{x}}=\mathrm{six.4}\\ \overline{Y}=\frac{3+\mathrm{x}+3+\mathrm{half\; dozen}+8+12+\mathrm{ane}+4+9+14}{10}=\mathrm{vii}\end{array}$

Now calculate $x_i-\overline{\mathrm{10}}$ , $y_i-\overline{Y}$ , $\left(x_i-\overline{X}\right)\left(y_i-\overline{Y}\right)$ , and ${\left(x_i-\overline{\mathrm{Ten}}\right)}^2$ for each $i$ .

$i$	${\mathrm{ten}}_i$	$y_i$	$x_i-\overline{\mathrm{10}}$	$y_i-\overline{Y}$	$\left(x_i-\overline{X}\right)\left(y_i-\overline{Y}\right)$	${\left({\mathrm{10}}_i-\overline{X}\right)}^{\mathrm{ii}}$
$1$	$8$	$\mathrm{three}$	$\mathrm{i.6}$	$-4$	$-6.4$	$\mathrm{two.56}$
$\mathrm{two}$	$\mathrm{two}$	$10$	$-\mathrm{iv.four}$	$3$	$-\mathrm{thirteen.2}$	$\mathrm{xix.36}$
$3$	$11$	$3$	$4.6$	$-4$	$-\mathrm{18.iv}$	$\mathrm{21.sixteen}$
$4$	$6$	$6$	$-0.4$	$-\mathrm{one}$	$\mathrm{0.iv}$	$\mathrm{0.xvi}$
$5$	$\mathrm{v}$	$8$	$-\mathrm{1.iv}$	$1$	$-\mathrm{1.four}$	$1.96$
$6$	$4$	$12$	$-\mathrm{two.4}$	$5$	$-12$	$5.76$
$\mathrm{vii}$	$12$	$\mathrm{ane}$	$5.6$	$-6$	$-\mathrm{33.half\; dozen}$	$31.36$
$8$	$9$	$\mathrm{four}$	$\mathrm{ii.6}$	$-3$	$-\mathrm{7.viii}$	$\mathrm{vi.76}$
$\mathrm{ix}$	$6$	$9$	$-0.4$	$2$	$-\mathrm{0.eight}$	$0.16$
$10$	$\mathrm{i}$	$14$	$-\mathrm{five.4}$	$7$	$-37.8$	$29.16$
					$\begin{array}{l}{\displaystyle \sum _{i=1}^n\left(x_i-\overline{\mathrm{Ten}}\right)\left(y_i-\overline{Y}\right)}\\ =-131\end{array}$	$\begin{array}{l}{\displaystyle \sum _{i=\mathrm{one}}^{\mathrm{due\; north}}{\left(x_i-\overline{\mathrm{10}}\right)}^{\mathrm{two}}}\\ =118.4\end{array}$

Summate the slope.

$m=\frac{{\displaystyle \sum _{i=\mathrm{one}}^{\mathrm{due\; north}}\left(x_i-\overline{\mathrm{Ten}}\right)\left(y_i-\overline{Y}\right)}}{{\displaystyle \sum _{i=\mathrm{one}}^n{\left({\mathrm{10}}_i-\overline{\mathrm{10}}\right)}^{\mathrm{ii}}}}=\frac{-131}{\mathrm{118.four}}\approx -\mathrm{1.one}$

Summate the $y$ -intercept.

Utilise the formula to compute the $y$ -intercept.

$\begin{array}{l}b=\overline{Y}-\mathrm{one\; thousand}\overline{X}\\ =7-\left(-\mathrm{ane.1}\times \mathrm{6.four}\right)\\ =\mathrm{vii}+7.04\\ \approx 14.0\end{array}$

Use the gradient and $y$ -intercept to course the equation of the line of best fit.

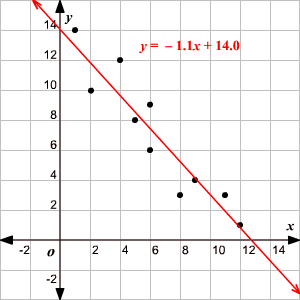
The slope of the line is $-\mathrm{one.1}$ and the $y$ -intercept is $14.0$ .

Therefore, the equation is $y=-\mathrm{1.ane}\mathrm{10}+14.0$ .

Draw the line on the scatter plot.

Slope Of Best Fit Line,

Source: https://www.varsitytutors.com/hotmath/hotmath_help/topics/line-of-best-fit

Posted by: matneyfror1958.blogspot.com

Share this post